The complex Mo(CO)3[P(OMe)3]3 has octahedral coordination geometry and can adopt two isomeric forms as shown (for convenience only the P atoms of the P(OMe)3 groups are indicated).
| What are the point groups of these two isomeric structures? | 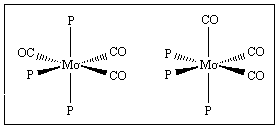
|
A sample of the complex was synthesized and its IR spectrum was found to include vibrations at 1900, 1925 and 2000 cm-1.
Use group theory to predict the number of IR and Raman active CO stretching vibrations you would expect to observe for both isomers and hence deduce the stereochemistry of the actual product.
Meridonal Isomer (Mer) — C2v
- Using arrows along each Mo—CO bond as a basis, obtain a representation.
- Reduce the representation
- The vibrational modes can be assessed to determine whether they are IR and/or Raman active.
C2v E C2 σv(xz) σv′(yz) A1 1 1 1 1 z x2,y2,z2 A2 1 1 -1 -1 Rz xy B1 1 -1 1 -1 x,Ry xz B2 1 -1 -1 1 y,Rx yz