Using the images in the table below, click on the F atom in the product which should be coloured red after successive clockwise rotations through 90° performed about the C4 axis in XeF4. (All the F atoms are identical - one has been coloured red merely for convenience!)
NB. The C4 operation performed two/three/four times is represented as C42/C43/C44 respectively.
| Rotation | Clickable Image | Corresponding Answer |
|---|---|---|
| C4 | 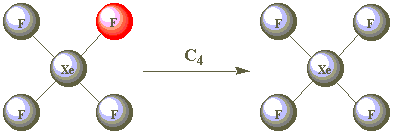 | |
| C42 | 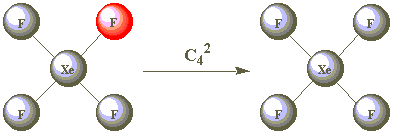 | |
| C43 | 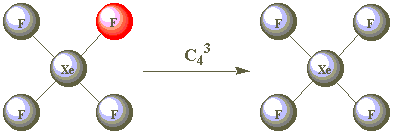 | |
| C44 | 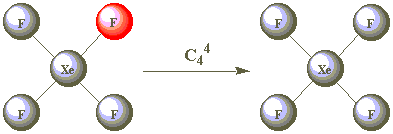 |
As all the F atoms are identical, the result of C42 is also indistinguishable from the starting position. C42 is therefore a second operation associated with the C4 element. Are C43 and C44 other operations?
After performing C44 the molecule has now returned to its starting position. What symmetry operation is this equivalent to? Can you think of an operation equivalent to C42 ?
The total number of independent symmetry operations that can be performed on a molecule is of fundamental importance. So as long as we consider all the symmetry elements (including E), we do not need to count operations (such as C42 and C44) that have equivalents. The C4 symmetry element therefore generates only two operations: C4 and C43.
| All planar molecules have a mirror plane σ. The operation performed twice (σ2) is equivalent to the operation E (no change), so the element σ generates a single operation. | 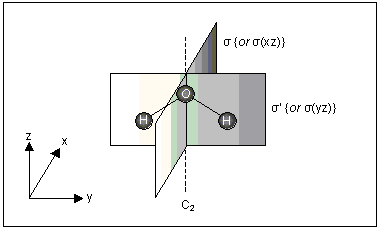 | ||
| The H2O molecule has two σ planes and a C2 axis. This molecule therefore has four symmetry elements: E, C2, σ and σ′. | |||
| Each of these elements generates a single operation, and these operations are known by the same symbols: E, C2, σ and σ′. |
We shall see later that the correct determination of the symmetry operations that can be performed on a molecule is essential for the application of group theory.
| Workshop Contents | Return to top of page | Next (Exercise 2) |